Hagsveiflugreining Kuznets

Kuznets hafði áhuga á hagsveiflum. Hann hugsaði sér þjóðarframleiðslu:

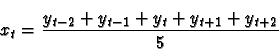
y_t = logaritma þjóðarframleiðslu á ári t

hann hafði ekki áhuga á skammtímasveiflum svo hann ákvað að taka 5 ára hreyfanlegt meðaltal til að jafna út skammtímahreyfingum:

$$\begin{eqnarray*}x_t = \frac {y_{t-2}+y_{t-1}+y_t+y_{t+1}+y_{t+2} } 5\end{eqnarray*}$$ síðan ætlaði hann að skoða hagvöxtinn svo hann tók mismun, hann taldi 10-ára mismun hæfilegan:

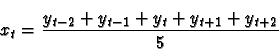
g_t = x_t+5-x_t-5

Niðurstaða hans var að margar hagraðir hefður ca. 20 ára sveiflu.

Hvað var það sem Kuznets gerði?
 
 

g_t er filtreruð útgáfa af  y_t
 

g_t = A(B) y_t

þar sem

$$\begin{eqnarray*}By_t = y_{t-1} \quad \quad \textrm{Backward operator}\end{eqnarray*}$$ Önnur tákn fyrir B eru L, q, z, q^-1.

Hjá Kuznets er

$$\begin{eqnarray*}A(B) = (B^5-B^{-5}) ( \frac {B^{-2}+B^{-1}+1+B+B^2} 5)\end{eqnarray*}$$ Þetta er dæmi um línulegt filter. Hvað gerir svona filter við tímaröð?

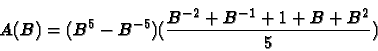
Það skoðar röðina í gegnum ákveðin gleraugu. Gleraugu þar sem ákveðnum hlutum er sleppt í gegn.

Hér er spectral teoría heppileg til að skilja hvað þessi gleraugu eru að gera.

Spektur raðar y_t er fall af tíðninni w:

$$\begin{eqnarray*}f_y(w) = \sigma^2 (1 + 2 \sum_{i=1}^\infty \rho_y(k)cos(kw) & -\pi < w < \pi\end{eqnarray*}$$ þar sem $\rho_y(k)$ er sjálffylgnifall raðarinnar y_t.

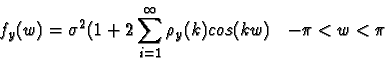
Fallið f_y(w) er eins konar sveiflusjá sem sundurliðar breytileika raðarinnar y_t niður á einstakar tíðnir (bylgjur). Ef fallið hefur topp í ákveðnum punkti w₀ er það túlkað sem að mikill hluti breytileikans sé vegna sveiflu af lengd:

$$\begin{eqnarray*}\frac {2\pi} {w_0}\end{eqnarray*}$$ Munið eftir reiknireglu um varíans, ef a er fasti og X er hending (random breyta)

V(aX) = a² V(X)

Hjá Kuznets var:

g_t = A(B) y_t

Við höfum útgáfu af áðurnefndri reiknireglu um varíans fasta sinnum hending fyrir filtreraðar tímaraðir:

f_g(w) = |A(e^-iw)|² f_y(w)

þar sem f_g(w) og f_y(w) eru spektur fyrir g_t og y_t. Þessi formúla segir því hvernig bylgjur í y_t verða í g_t.

Fallið:

H(w) = |A(e^-iw)|²

er stundum nefnt tilfærslufall (transfer function), eða filter fall. Sé það teiknað upp má skilja eðli þeirra gleraugna sem búin hafa verið til með filternu.

Með þríhyrninga-algebru má sjá að filterið hjá Kuznets var:

$$\begin{eqnarray*}H(w) = \left [ \frac {2 sin(5w) sin(5w/2)}{5sin(w/2)} \right ]^2\end{eqnarray*}$$ Sjá mynd: Á mynd er H(w) sýnt. Túlkun er sú að filter Kuznets sleppir í gegnum sig miklu af 20.3 ára sveiflu. Ef hvítt suð hefði verið sett inn hefði komið út eitthvað sem einkenndist af rúmlega 20 ára sveiflu.

Figure 1: Kuznets filter

2001-03-27