Líkindafræði (Probabilty ) + Ályktunarfræði (Inference)
Líkanasmíði (modelling): Einfölduð mynd af raunveruleika
Ályktun = líkan + gögn
Upprifjun Líkindafræði, nokkur hugtök
Tilraun, atburður, líkur
Reiknireglur um líkur, óháðir atburði, skilyrtar líkur, Regla Bayes
Random breyta = Hending (e. Random variable)
Eiginleikar hendinga, samfelldar/sundurslitnar
Dreifing: Dreififall(cdf) , þéttifall (density, pfd), líkandafall (pmf=probability mass function)
Lýsitölur fyrir dreifingar, væntanleg gildi (expected value), dreifni (variance), miðgildi (median ) o.s.frv.
Margvíðar hendingar, samand hendinga, fylgni.
Reiknireglur fyrir væntanlegt gildi og varíans(dreifni)
Ýmsar dreifingar, hvers vegna hafa þær nafn, verkefni.
Ályktunarfræði, Mat (punktmat, bilmat) Kenningaprófanir
Mat, Punktmat, Metill(estimator), hlutdrægni(bias),
samkvæmni ( consistency), nýtni (efficiency)
Mat, Bilmat, öryggismörk (confidence limits).
Kenningaprófanir, Núllkenning, valkostur, villa I, villa II, marktækni(significance), styrkur (power) Verkefni
Tveir skólar ályktunarfræði, Hefðbundinn(tíðni-skóli),
Bayesian skóli.
Aðhvarf(regression) og fylgni(correlation)
Ýmsar tegundir af breytum.
Aðhvarf meðs einni skýristærð,
aðhvarf með mörgum skýristærðum,
tengsl við ANOVA,
tengsl við samanburð meðaltala Verkefni
Tegundir parametra (í. stika), main effects, interactions, intercept, slope. Túlkanir.
Nokkur atriði um matsaðferðir.
GLIM fjölskyldan
Venjuleg ANOVA, aðhvarfslíkön,
Tilraun (experiment), aðgerð sem gefur útkomu
Ùtkoma óviss, atburður = mengi af útkomum
Mengja-stærðfræði hentug,
A 
= atburðurinn A og B
A 
B = atburðurinn A eða B (geta verið báðir)
= mengi af öllum mögulegum útkomum
Líkur
P vörpun sem úthlutar atburði tölu á milli 0 og 1.
P(A B) = P(A) + P(B) - P(A 
B)
Óháðir (independent) atburðir
P(A B) = P(A) P(B)
skilyrtar líkur (conditional probability)
A 
B = atburðurinn A gefið atburðurinn B
P(A B) = P(A B)/P(B)
regla Bayes
P(A B) = P(B A) P(A)/P(B)
Dæmi: Á að mótefnamæla population?
Segjum 250.000 manna population,
prevalence = 500
sensitivity = specificty =0.95
reiknið P(S=+ T=+)
svar: P(S=+ T=+)*250.000
= mörg þúsund
Dreififall(Cdf) hendingar
F(x) = P(X 
x) (ath. stórt og lítið x)
þéttifall(density, pdf) líkindamassafall (pmf)
f(x) = F
(x) ef X er samfelld
f(x) = P(X=x) ef X er sundurslitin
Lýsitölur fyrir hendingar
E(X) = expected value =væntanlegt gildi
E(X) = 
x f(x) dx ef X er samfelld
E(X) = 
x f(x) ef X er sundurslitin
V(X) = variance X = dreifni X
V(X) = 
= E(X-E(X))
= staðalfrávik X
x
= q-kvantíll 
F(x)=q
Margvíðar hendingar (multivariate random variables)
F(x,y) = P(X 
x Y y)
f(x,y) = F-diffrað fyrir samfelldar hendingar
f(x,y) = P(X=x Y=y) fyrir sundurslitnar
X og Y óháðar F(x,y)=F(x)F(y)
YX hefur dreififall F
(yx)
Reiknireglur væntanlegt gildi og varíans
E(aX) = a E(X)
V(aX) = aV(X)
Fylkja-algebra (matrix-algebra mjög þægileg
Ef X er vektor af hendingum
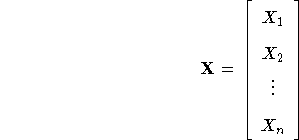
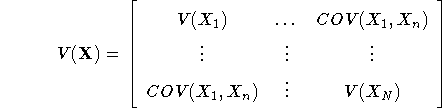
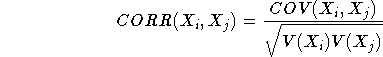
Nokkrar tegundur sundurslitinna (discrete) dreifinga
Bernoulli (p)
Binomial, B(n,p)
Poisson, 
Geometric (p)
Negatív binomial (r,p)
Uniform (a,b)
Nokkrar tegundir samfelldra hendinga
Uniform (a,b)
Exponential
Gamma (r, )
Normal N( 
, 
)
(k)
t(k) cauchy=t(1)
F(n,m)
Verkefni
Búið til 30 mælingar úr a) exponential dreifingu með meðaltal
180, b) N(180,7) og c) cauchy með miðgildi 180, og 5% meira en 190.
Reiknið úrtaksmeðaltal, úrtaksstaðalfrávik og staðalfrávik úrtaksmeðaltalsins.
Endurtakið fyrir úrtaksstærð 300 og 3000.
Verkefni Búið til 30 mælingar úr normaldreifingu með meðaltal 0 og staðalfrávik 1. Reiknið 95Endurtakið 50-1000 sinnum. Notið tölvu og viðeigandi forrit. T.d. EXCEL eða einhvern annan töflureikni.
Verkefni
Búið til 30 mælingar úr normaldreifingu með meðaltal 0 og
staðalfrávik 1. Prófið kenninguna að meðaltalið sé 0 og gangið út
frá að vitað sé að staðalfrávik sé 1. Er kenningunni hafnað miðað
við 
=0.05? Enrdurtakið 50-1000 sinnum.
Verkefni
Búið til 30 mælingar úr normaldreifingu með meðaltal 0.2 og
staðalfrávik 1. Prófið kenninguna að meðaltalið sé 0 og gangið út
frá að vitað sé að staðalfrávik sé 1. Er kenningunni hafnað miðað
við =0.05? Enrdurtakið 50-1000 sinnum.
Verkefni
Búið til 30 mælingar úr normaldreifingu með meðaltal 0.4 og
staðalfrávik 1. Prófið kenninguna að meðaltalið sé 0 og gangið út
frá að vitað sé að staðalfrávik sé 1. Er kenningunni hafnað miðað
við =0.05? Enrdurtakið 50-1000 sinnum.
Nokkur atriði um logistic regression
Það sem meta á eru líkur á ákveðnum atburði, t.d. bilun sjúkdómi eða þess háttar. Köllum þá breytu Y. p=P(Y=1), 1-p=P(Y=0). Gerum ráð fyrir að
p= e
/ (1 + e)
sem er jafngilt og
log(p/(1-p)) = 
Likelihood-fall fyrir eina mælingu er:
L(
| y,x) = p
(1-p)
log(L) = y log(p) + (1-y) log (1 - p)
Fyrir n óháðar mælingar er log-likelihood fallið því
( y
log(p) + (1-y) log (1-p))
p = e
/ (1 + e)
Nokkur atriði um survival-greiningu.
Helstu hugtök S(t) survival fall, S(t) = 1 - F(t) þar sem hendining T er endingartími þess sem rannsaka skal.
h(t) hazard fall, h(t) = f(t)/S(t)
H(t) cumulative hazard fall, H(t) = 
h(s) ds
Dæmi, Líftími exponential dreifður, f(t) = e
þá er S(t) = 1 - F(t) = 1 - (1 - e) = e
og
h(t) = f(t)/S(t) = e /e =
H(t) = t
Censoring, það liggur í hlutarins eðli að við getum ekki séð heildar feril hvers og eins. Það munu verða margir sem við vitum ekki dánardægur á. Til eru ýmsar tegundir af censoring.
Aðferðir til að meta survival feril. E.t.v. best þekkt Kaplan-Meier og Flemming-Harrington. Einni hugsanlegt að negla niður fyrirfram ákveðið form eins og t.d. Weibull-dreifingu.
Oft er S(t) sjálft ekki aðaláhugamálið heldur samanburður ýmissa hópa og áhrif skýristærða.
Get gefið mér fjölskyldu af líftímadreifingum, weibull, log-normal, log-logistic o.s.frv. og síðan framkvæmd einhvers konar aðhvarfsgreiningu. (eins konar GLM)
Cox-regression, gengur út á að hægt sé að þátta hazardfallið h(t)á á eftirfarandi hátt
h(t,x) = hazard fall fyrir einstakling með eiginleika x
= h(t) exp(x)
Þ.e. að ein grunn-hazard lína gildi fyrir alla og síðan sé munurinn
eingöngu fólginn í þættinum exp(x).
Nokkur atriði um tölfræðilega líkanagerð
Skilgreina markmið
Skilgreina áhugaverð tengsl, átta sig á truflandi þáttum
Við experimental aðstæður, kynna sér experimental design til að fá hámarksupplýsingar út úr mælingunum.
Setja fram hugsanlegt líkan, þ.e. átta sig á hugsanlegri dreifingu mælinga, hugsanlegu formi líkans.
Meta Líkan, t.d. með maximum-likelihood aðferð.
Framkvæma ítarlega diagnostics, leifaskoðun (residual analysis). Àtta sig á að hvernig líkan misstígur sig. Átta sig á outliers og influential observations. Athugið að til eru margs konar leifar, í venjulegum normal líkönum, t.d. least-squares residuals og recursive residuals. Ì GLIM og survival eru margskonar leifar.
Ef líkan stendst skoðun túlka niðurstöður. Varist over-fitting, þ.e. að finna líkan sem hentar mældum gögnum afar vel en gæti misstígið sig illa ef því væri beitt á annað gagnasett. Almennt gildir að velja skuli líkönin sem minnst (principle of parsimony)